
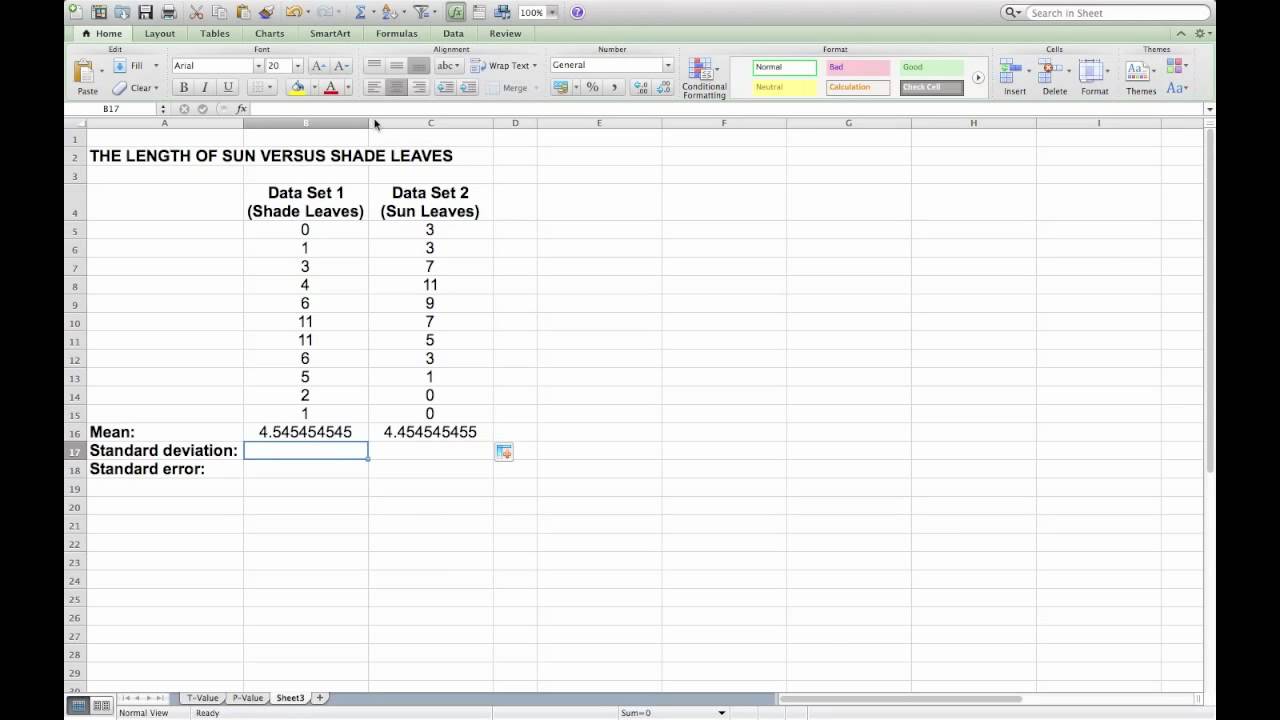
Note: you already knew this answer (see step 5 under STDEV.P). The VAR.P function below calculates the variance based on the entire population. Sometimes it's easier to use the variance when solving statistical problems.ġ. Variance is the square of the standard deviation. Note: why do we divide by n - 1 instead of by n when we estimate the standard deviation based on a sample? Bessel's correction states that dividing by n-1 instead of by n gives a better estimation of the standard deviation. Fortunately, the STDEV.S function in Excel can execute all these steps for you. Repeat steps 1-5 above but at step 5 divide by n-1 instead of N.ģ. The STDEV.S function uses the following formula: You only have the test scores of 5 students. For example, you're teaching a large group of students. The STDEV.S function (the S stands for Sample) in Excel estimates the standard deviation based on a sample. Fortunately, the STDEV.P function in Excel can execute all these steps for you. Divide by the number of data points (N = 5).ħ. For each number, calculate the distance to the mean.ģ. The STDEV.P function uses the following formula: The entire population consists of 5 data points. You have the test scores of all students. For example, you're teaching a group of 5 students.
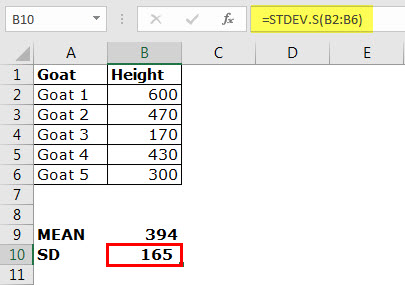
The STDEV.P function (the P stands for Population) in Excel calculates the standard deviation based on the entire population. As a result, the numbers have a high standard deviation. The numbers below also have a mean (average) of 10.Įxplanation: the numbers are spread out. As a result, the numbers have a low standard deviation.ģ. The numbers below also have a mean (average) of 10.Įxplanation: the numbers are close to the mean.


 0 kommentar(er)
0 kommentar(er)
